33. In search of harmony

Systems to understand the world

A ‘system’ is defined here as a collection of mutual related symbols, which are regarded as a unity. A system is an effort to bring order in a multitude of (abstract) possibilities. The design of ‘world-systems’ – as a conscious effort to develop and define an understanding of the world – can be historically traced in the transition-areas between multitude and unity and vice versa. The areas to look for in a quadralectic communication are, for that matter, situated on both sites of the Third Quadrant (III) (fig. 214).

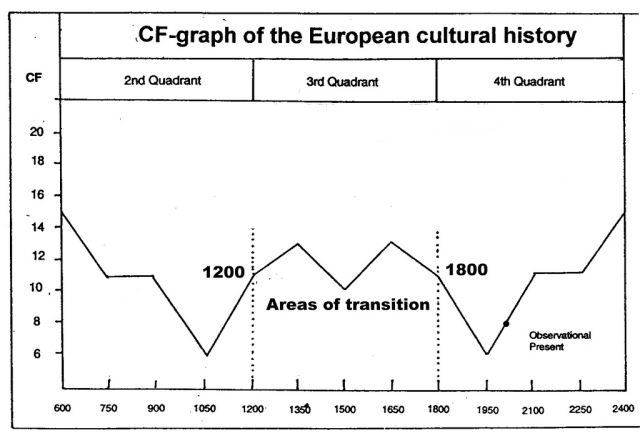Fig. 214 – Areas of transition in the European cultural history with a major change in division thinking. The CF (Communication Factor) is a measure for the ‘distance’ between the communication partners. Higher values (of the shift value CF) point to a remissio/ alienation and lower values indicate an intensio/attraction.

The special interest in the European cultural history should focus on the years 1200 and 1800, because they indicate the (subjective) beginning and end of the Third Quadrant (III). The system builders of the first transition period (1200 A.D.) were the Paris master Hugh of St. Victor (SCHNEIDER, 1933), Odo of Morimond, Theobald of Langres, Wilhelm of Auberive (Guillelmus de Alba Ripa) and others. They developed, with or without mythical means, a kind of general overview of life and history in the spirit of partitioning.

Hugh of St. Victor placed, in his ‘Eruditio didiscalica‘ (‘Didascalicon‘, a medieval guide to the arts), the mechanical and ‘artes liberales‘ side by side (DUBY, 1976/1984). The book was an elaboration of Hrabanus Maurus’ ‘De Doctrina‘ (ROBERTSON, 1951) (fig. 215).

Fig. 215 – Hrabanus Maurus (c. 780 – 856) is seen here to the left, presenting his work to Otgar of Mainz. Hrabanus works were heavily used by the system builders of the first wave in the twelfth century. In: KUNSTMANN (1841).

Hugh of St. Victor developed a science of numbers, which could be applied in a practical sense (like architecture). Odo of Morimond was interested in the ‘mysteria numerorum‘ (1147) and Theobald stated: ‘De quator modis, quibus significationes numerorum aperiuntur‘ (Paris, Nat. lat. 2583 (XIII), f. 25 – 35). Wilhelm of Auberive was attracted by ‘de significationes numerorum‘ (BEAUJOUAN, 1961). They all tried to create a deeper insight by numbers, the building stones of a divided universe, which could be measured and quantified.

The list of system-builders around the other transition-point (of the Third Quadrant) in the year 1800, is even longer. The following representatives are arbitrary chosen, since most scientists at that time could be called ‘system builders’.

A good illustration is Charles FOURIER (1772 – 1837), who developed his ‘Theorie des quatre mouvements et des destinées generales‘ (1808/ 1841). There is an analogy between four types of movements, according to Fourier: 1. Material (materiel); 2. Organic (organique); 3. Animal (animal) and 4. Social (social) or, like he called it, an ‘analogie des modifications de la matière avec la théorie mathematique des passions de l’homme et des animaux.’ His ‘ordre des creations‘ (order of creation) comprised four phases, which were regarded as ‘universal’ (fig. 216).

Fig. 216 – Theorie des Quatre Mouvements et des Destinees Generales. In: FOURIER  (1841).

Fourier envisaged a quadruple method of division, which was applicable to all forms of creation:

1. Youth (Enfance ou incoherence ascendante).

This phase was subdivided in seven periods and lasted 1/16th of the human history, i.e. 5000 years. It ended with a sudden jump from chaos into harmony (‘saut de chaos en harmonie‘).

2. Gradual growing (Accroissement ou combinaison ascendante).

This phase consisted of nine periods with seven ‘creations harmoniques‘ lasting 4000 years. The total duration is 7/16th of the duration of (human) history or 35.000 years.

Halfway (because Fourier was still tied in the bonds of dualistic thinking) is an ‘apogée du bonheur’, which he called a ‘periode pivotale ou amphiharmonique‘ with a duration of about 8000 years.

3. Decline (Declin ou combinaison descente).

This phase also consisted of nine periods, with seven ‘creations harmoniques‘ (of 4000 years). Total duration is 7/16th of the human history or 35.000 years. The phase ended with a ‘saut d’harmonie en chaos‘.

4. Decay (Caducite ou incoherence descendante).

This last phase comprised seven periods, showing a ‘creation subversive posterieure‘. They are a mirror image of the first phase, but now there is a jump into chaos, agony and savagery, closing in a ‘series confusés‘. The duration of this period is 1/16th of the human history or 5000 years.

The ‘fin du monde animal et vegetal‘ takes place, according to Fourier, ‘apres une duree de 80.000 ans‘. In this case, he has not included the duration of 8000 years of his ‘periode pivotale‘.

The main line of thinking in Fourier’s book about the ‘Theorie des Quatre Mouvements‘ (composed in 1807) was an ascending (‘vibration ascendante‘) and a descending movement (‘vibration descendante‘) in the ‘Ordre des creations’ (Order of Creation). This formal two-sided symmetry pointed to a dualistic rather then a tetradic mind of Fourier as a creative social inventor.

The history of Fourier’s book indicated, that the writer was not always certain. He talked of a ‘ballon d’essai’ (fly a kite) and admitted that ‘la Theorie n’etait pas complète‘. He shelved the manuscript in 1808 because of the errors it contained (‘a cause des erreurs qu’il contenait‘). In another of his books from 1822 (‘Traite de l’Association domestique-agricole‘) he did not even mentioned the ‘Theorie de quatre mouvements‘.

The quaternary division of culture in ‘enfance, accroissement, declin et caducite‘ is, in fact, a two-fold division with an upward and downward movement. And usually if predictions are made within this context, the trend is downwards: we are in the third phase, in the decline (p. 133: ‘elle est actuellement en troisieme phase, en declin‘). And Fourier also knew the reason, because of its social progress (‘Une societe peut tomber en declin par l’effet de ses progres sociaux‘).

MANUEL & MANUEL (1979) devoted in their inspiring book on the ‘Utopian Thought in the Western World’ a chapter to Charles Fourier (Ch. 27). They noted that ‘Fourier was constantly collecting, counting, cataloguing, and analyzing’ (p. 642). Their verdict of his personality was explicit: ‘Paranoid elements are almost always latent in the great structure-builders; in Fourier, they rise to the surface – nothing is hidden’.

When Fourier, as a young traveling salesman, noticed the great difference in price of apples in Paris and the countryside, he saw himself as part of a great tradition: ‘There had been four apples in the world: two were destined to sow discord and two to create concord. While Adam and Paris had brought misery to mankind, Newton’s apple had inspired the discovery of the basic law of attraction, which governs the physical motion, and its complement, Fourier’s apple, had moved him to formulate the law of passionate attraction, which would inaugurate universal happiness.’

Charles Fourier saw himself as a drafter of the general theory of harmony and his system of thought was based on an ‘attraction of feelings‘, which existed between human beings (in analogy with the attraction of material parts). The attention to emotions (feelings) is – despite his confusing way of presentation – the key to the Fourth Quadrant in the European civilization.

Fourier distinguished four main types of feelings in his analysis of the human mind:

1. Feelings of unity; this type was called (with a neologism) the unityisme. It was presented as a tree trunk, with three main branches:

2.  Feelings of luxury; linked with the desires of the five senses.

3. Feelings of the group or ‘affective passions’ consisting of four groups:

—————-  3.1. need for respect (honor)

—————- 3.2. need for friendship

—————- 3.3. need for love

—————- 3.4. need for parenthood

4. Feelings of continuity, also called the serial or distributive, consisting of three groups:

—————  4.1. need to arrange (concordant)

————— 4.2. need to intrigue (discordant)

————— 4.3. need for variety

The French naturalist and zoologist Georges Cuvier (1769 – 1832) embodied another delegate of the new era. He arrived in Paris in 1795 and was eager to find a solution for the evolutionary problems of animals. He proposed, that the four main groups in nature – vertebrates, molluscs, articulata (insects) and ‘radiata‘ (radial-symmetric animals) – developed themselves every time anew after a major catastrophe. The fourfold division was, according to Cuvier, the ‘ideal specification’ of nature (TOULMIN & GOODFIELD, 1965).

Cuvier’s rival, Lamarck (1744 – 1829), suggested – in a lecture in the year 1800 – a different solution. Not the catastrophes caused the changes, but the species changed themselves. He pointed to the four classes in the animal kingdom (mammals, birds, reptiles and fish) and their decreasing complexity. They could  adapt themselves (within the classes) to changing circumstances. It is curious to note, that the term ‘biology’ was first used in the year 1800 to describe the science of plant- and animal kingdom (JORDANOVA, 1984). Apparently, the need for such a word arose at the time that the study of nature became a serious matter.

Order in nature was also sought in the classification of the rocks. Robert Jameson (1774 – 1854), geologist and professor of natural history at the University of Edinburgh, gave in his book ‘Elements of Geognosy’ (1808; SWEET, 1976) four main groups:

————–  1. Primitive

————–  2. Transition/Floetz

————–  3. Alluvial

————–  4. Volcanic

The then-known (23) minerals were grouped according to age:

1. the oldest primitieve formations (molybdena, menachine, tin, scheele, cerium, tantalium, uran, chrome, bismuth);

2. old, primitive formations and newer mountains (arsenic, cobalt, nickel, silver, copper);

3. middle period (newer primitive, transition and old floetz (sedimentairy) rocks (gold, sylvan, antimony, manganese);

4. later period (lead, zinc, mercury). Iron is finally found in every rock (and therefore very young).

The name ‘geology’ was – just like ‘biology’ – invented in the first years of the nineteenth century, and won supremacy over the simultaneously introduced word ‘geognosy‘.

A clear exposé of the philosophical aspects in the earth sciences around 1800 was written by Jay GOULD (1987). His book ‘Time’s Arrow – Time’s Cycle‘ proved convincingly, that James Hutton (1726 – 1797), and his book on ‘The Theory of the Earth‘ (1795), searched for an ‘a priori‘ of the changes, which took place in the history of the earth. Hutton’s quest was, in quadralectic terms, a discovery of the First Quadrant (I) – where the ‘telos‘ (or ultimate meaning) of Aristotle was situated. Gould rightly suggested, that this ‘telos‘ was, in Hutton’s treatment, just another word for ‘God’.

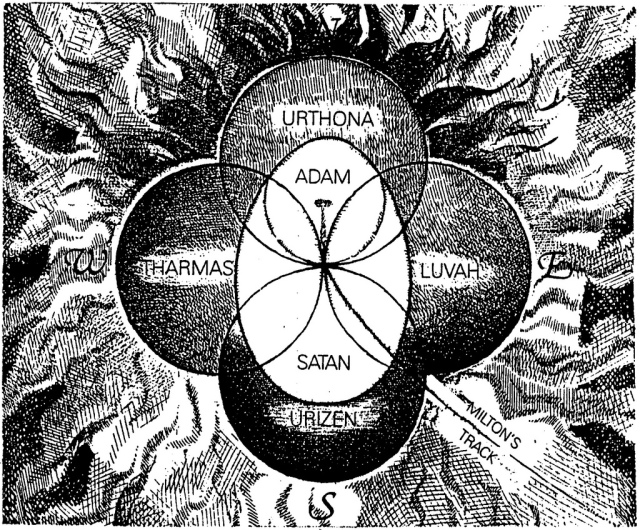
The early nineteenth century was searching for new spiritual ground. The poem of William Blake, titled ‘The Four Zoas‘ (written between 1796 and Blake’s death in 1827) was such an effort. The poem described his own mythology in eleven parts (Night I – XI)(WILKIE & JOHNSON, 1978).

Blake devised a universe of four Zoas (spheres), being representative of the primordial human qualities (fig. 217). The Four Zoas were gathered around the throne of Albion (the archetypal human being). Within the ‘Mundane Egg‘ (the white part in fig. 217) there is a clash between Urizen (Ratio), Luvah (Passion) and Tharmas (Instinct), which is reconciled by the forces of Imagination in Urthona (the capacity to be creative and imaginative).

Four Mighty Ones are in every Man: a Perfect Unity

Cannot Exist. but from the Universal Brotherhood of Eden

The Universal Man. To Whom be Glory Evermore Amen

Fig. 217  – The spiritual pilgrimage of the poet Milton by William Blake. By traversing the territory of Satan, he comes face to face with Adam, where he finds the ‘Doors of Perception’ wide open.

A more scientific attempt of system building was made by the German philosopher F.J.W. von Schelling (1775 – 1854), in his ‘Erster Entwurf eines Systems der Naturphilosophie’, published in 1799. ‘Conquering the multitude’ was his first aim. He continued a line of thinking, initiated by John Brown (1735/36 – 1788) in his book ‘Elementae medicinae’ (1780). Brown’s research led to the conclusion that the movement of the multitude (observed in microscopic small animals) was governed by ‘incitabilitas‘ (excitability). The book by the Scottish physician became only known on the continent after a decade. Brown’s theory caused then a stir in scientific circles. More then two-hundred publications alone were issued in Germany between 1796 – 1808 (SCHULLIAN, 1960). The ‘Brownian movements’, as they were later called, represented a form of organized chaos, initiated by an outside influence (‘Leben eine von aussen erzwungener Zustand‘).

Von Schelling was aware of these results, and he emphasized the relation between receptivity (of sensibility) and irritability. This relation offered the key to order the multitude (of movements). Cause and effect were connected in a logical way.

PRIGOGINE & STENGERS (1985) followed this line of thought – the creation of order in chaos – in modern times. Also the study of ‘fractals‘, as initiated by MANDELBROT (1982), has to do with the description of ‘chaos’. Mandelbrot called Brownian movements ‘fractal sets’ and stated that ‘the physical Brownian motion is a natural fractal’.

Fig. 218 – Fractals from the book ‘The Beauty of Fractals’ by H.O. Peitgen and P.H. Richter (1968). These mathematical creations offer a better understanding of the seemingly haphazard movements, which take place in fluids and gases in nature.

Benoit Mandelbrot (1924 – 2010) provided an example of the ‘new’ visibility in the representation of a coastline on a map. The boundary between sea and land is – if mapped – an approximation, related to the scale of the map. It is always possible to go into more detail. The representation of reality is a matter of scale, reaching into infinity. Mandelbrot introduced the term ‘fractal‘, referring to the irregular and fragmented character of nature (fig. 218). The name is opposed to the denomination ‘algebra‘ – which is derived from the Arabic ‘jaraba’, meaning joining together. It was described as a ‘non-topological aspect of form’. The fractal is, in a quadralectic setting, the characterization of an invisible ‘fact’ in the Fourth Quadrant. This type of ‘visible invisibility (of the multitude)’ is astounding, in particular, for those who think in opposites.

‘I see it, but I don’t believe it!’

wrote Georg Cantor (1845 – 1918) to his fellow mathematician Richard Dedekind (1831 – 1916) in his letter of June 29, 1877. It was a reaction to his success to map a surface onto a line in such a way that each point of the surface corresponded to one point of the line (and reciprocally that to each point of the line one point of the surface could be related). He arrived at a correlation, which uniquely mapped the x-variables onto y in terms of four equations (DAUBEN, 1979; p. 55).

The work of Cantor is of importance, because it explored – in a mathematical way – the infinities (of the Fourth Quadrant). He got a glimpse of the incredible depth of vision, which is possible if the quadralectic way of thinking is realized to its full extent. Cantor pointed to the difference between Aristotle and Epicurus with respect to the subject of the continuum and its consistency.

Aristotle, he said, believed in a continuum composed of parts, which were divisible without limit, while Epicurus regarded the continuum as a synthesis from atoms, which were imagined as finite entities. In a modern, quadralectic, sense this observed opposition is a discussion about the place of the entity ‘continuum’ in the visible spectrum of the Fourth Quadrant. Aristotle placed it in the Second ‘Quadrant’ (of the Fourth Quadrant; IV, 2), and Epicurus positioned the continuum in the Third ‘Quadrant’ (IV, 3)

Cantor himself aimed at a position in the Fourth ‘Quadrant’ (of the Fourth Quadrant; IV, 4), the ultimate position of any visible continuum before it disappears in the ‘absolute’ invisibility of the (following) First Quadrant. He objected to the compromise of Thomas Aquinas, who believed that the continuum must be composed neither of infinitely many nor of a finite number of parts but of no parts whatsoever. The continuum is, in Cantor’s view, not an indivisible concept or an a priori intuition. He refused to place the continuum in the First Quadrant, because in that position it would defy all analysis. It would relegate the problem of the continuum to the level of a religious dogma. Instead he insisted to treat the subject as a ‘mathematisch-logischen Begriff’ (CANTOR, 1883; p. 119).

Any system to understand the world, in a modern sense, should include all four aspects of visibility. The quest for ultimate explanation – as researched by John D. BARROW (1991) in his book ‘Theories of Everything’ – has to take depth of division into account. The great Unifying Theory, to which Einstein devoted himself in the latter part of his life, is an effort to eliminate division from nature. Even Einstein had, just like Cantor before him, to admit defeat here. The main forces of nature are four in number: the gravitational force, the electromagnetic force, the weak interaction and the strong interaction. They are related to the position of the observer and the distance taken from nature. As long as the observer – and therefore, the division – exists, the ultimate unity will remain a fiction.

—

BARROW, John D. (1991). Theories of Everything. The Quest for Ultimate Explanation. Oxford University Press/Vintage, London. ISBN 0 09 998380 X

BEAUJOUAN, Guy (1961). Le symbolisme des nombres a l’epoque  romane.  pp. 159 – 169 in: Cahiers de civilisation medievale, 4.

CANTOR, George (1883). Grundlagen einer allgemeinen Mannigfaltigkeitslehre.  Ein mathematisch-philosophischer Versuch in der Lehre des Unendlichen. B.G. Teubner, Leipzig.

DAUBEN, Joseph W. (1979). Georg Cantor. His Mathematics and Philosophy of  the Infinite. Harvard University Press, Cambridge, Massachusetts/London. ISBN 0-674- 34871-0

DUBY,  Georges (1976/1984). De kathedralenbouwers: portret van de middeleeuwse maatschappij 980 – 1420. Galllimard, Parijs/Agon, Amsterdam. ISBN 90 5157 134 8

FOURIER, Charles (1808/1841). Theorie des Quatre Mouvements et des Destinees Generales. Tome Premier. Oeuvres Completes de Ch. Fourier, Aux Bureau de la Phalange, Paris.

GOULD,  Stephen Jay (1987).  Time’s Arrow – Time’s Cycle. Harvard University Press, Cambridge (Mass.).

JORDANOVA, L.J. (1984). Lamarck. Oxford University Press, Oxford. ISBN 0-19-287588-4

KUNSTMANN, Friedrich (1841). Hrabanus Magnentius Maurus. Eine historische Monographie. Kirchheim, Schott & Thielmann, Mainz

MANDELBROT, Benoit B.  (1982). The Fractal Geometry of Nature.  W.H. Freeman, San Francisco. ISBN 0716711869

MANUEL,  F.E.  & MANUEL,  F.P.  (1979). Utopian Thought in the Western  World.  The Belknap Press of Harvard University Press, Cambridge, Massachusetts. ISBN 0-674- 93186-6

PEITGEN, Heinz O. & RICHTER, Peter H. (1986). The Beauty of Fractals.  Images of Complex Dynamical Systems. Springer Verlag, Berlin. ISBN 0-387-15851-0

PRIGOGINE, Ilya & STENGERS, Isabelle (1985). Orde uit chaos. De nieuwe dialoog tussen de mens en de natuur (tr.: Order Out of Chaos). Uitgeverij Bert Bakker, Amsterdam. ISBN 90 351 0212 6

ROBERTSON Jr., D.W. (1951). The Doctrine of Charity in Medieval Literary Gardens: A Topical Approach through Symbolism and Allegory. Speculum, A Journal of Medieval Studies. Vol. 26, 1951.

SCHNEIDER,  W.A. (1933). Geschichte und Geschichtsphilosophie bei Hugo von St. Victor. Münstersche Beiträge zur Geschichtsforschung. III. Folge, II. Heft, Verlag der Universitäts-Buchhandlung Franz  Coppenrath, Münster (Westfalen).

SCHULLIAN, Dorothy M. (1960). Alexander von Humboldt and Brunonianism. Notes and Events. Pp. 75 – 77 in: Journal of Medical and Allied Sciences. Oxford Journals. Volume XV, Issue 1.

SWEET,  Jessie M. (Intr.)(1976). The Wernerian Theory of the Neptunian Origin of Rocks.  Facs.  Repr. Elements of Geognosy, 1808. Robert JAMESON. Hafner Press, New York/Collier MacMillan Publ., London. LCCC 75-43364

TOULMIN, Stephen & GOODFIELD, June (1965). The Discovery of Time. Penguin Books Ltd., Harmondsworth, Middlesex, England.

WILKIE,  Brian & JOHNSON,  Mary Lynn (1978).  Blake’s Four  Zoas.  The  Design of a Dream. Harvard University Press, Cambridge, Massachusetts and London. ISBN 0-674- 07645-1